Simio and Simulation: Modeling, Analysis, Applications - 7th Edition
Chapter 2 Basics of Queueing Theory
Many (not all) simulation models are of queueing systems representing a wide variety of real operations. For instance, patients arrive to an urgent-care clinic (i.e., they just show up randomly without appointments), and they all must first sign in, possibly after waiting in a line (or a queue) for a bit; see Figure 2.1.
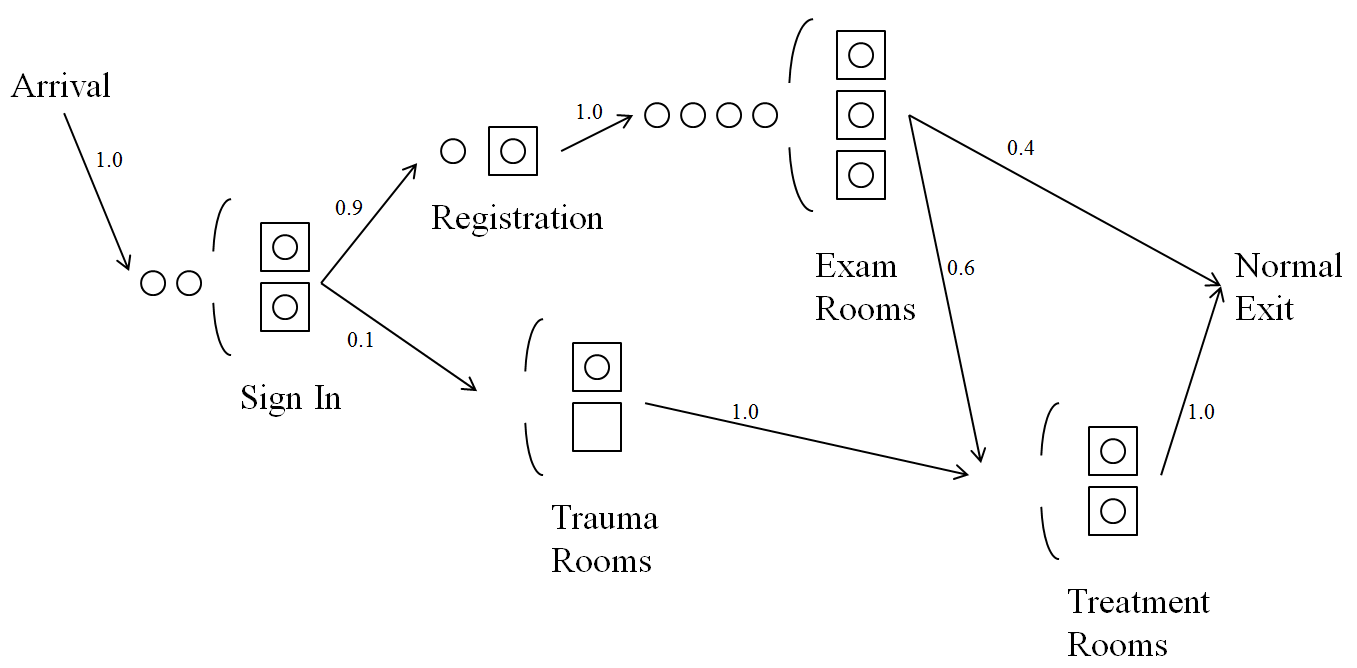
Figure 2.1: A queueing system representing and urgent-care clinic
After signing in, patients go either to registration or, if they’re seriously ill, go to a trauma room, and could have to wait in queue at either of those places too before being seen. Patients going to the Exam room then either exit the system, or go to a treatment room (maybe queueing there first) and then exit. The seriously ill patients that went to a trauma room then all go to a treatment room (possibly after queueing there too), and then they exit. Questions for designing and operating such a facility might include how many staff of which type to have on duty during which time periods, how big the waiting room should be, how patient waiting-room stays would be affected if the doctors and nurses decreased or increased the time they tend to spend with patients, what would happen if 10% more patients arrived, and what might be the impact of serving patients in an order according to some measure of acuity of their presented condition instead of first-come, first served.
This short chapter will cover just the basics of queueing theory (not queueing simulation), since familiarity with this material and the terminology is important for developing many simulation models. The relatively simple mathematical formulas from elementary queueing theory can also prove valuable for verification of simulation models of queueing systems (helping to determine that the simulations are correct). Queueing-theory models can do that by providing a benchmark against which simulation results can be compared, if the simulation model is simplified (probably unrealistically) to match the more stringent assumptions of queueing theory (e.g., assuming exponential probability distributions even though such is not true for the real system we’re simulating). If the (simplified) simulation model approximately agrees with the queueing-theoretic results, then we have better confidence that the simulation model’s logic, at least, is correct. As we develop our Simio simulation models in later chapters, we’ll do this repeatedly, which is helpful since simulation “code” can be quite complex and thus quite difficult to verify.
Queueing theory is an enormous subject, and has been studied mathematically since at least 1909, at first by A.K. Erlang in connection with how the recently-invented “telephone” systems in Copenhagen, Denmark might be designed and perform ((Erlang 1909), (Erlang 1917)). There are many entire books written on it (e.g., (Gross et al. 2008), (Kleinrock 1975)), as well as extensive chapters in more general books on probability and stochastic processes (e.g. (Ross 2010)) or on other application-oriented topics like manufacturing (e.g. (Askin and Standridge 1993)); a web search on “queueing theory” returned more than 1.4 million results. Thus, we make no attempt here to give any sort of complete treatment of the subject; rather, we’re just trying to introduce some terminology, give some basic results, contrast queueing theory with simulation via their relative strengths and weaknesses, and provide some specific formulas that we’ll use in later chapters to help verify our Simio simulation models.
In this chapter (and really, in the whole book), we assume that you’re already familiar with basic probability, including:
The foundational ideas of a probabilistic experiment, the sample space for the experiment, and events.
Random variables (RVs), both the discrete and continuous flavors.
Distributions of RVs — probability mass functions (PMFs) for discrete, probability density functions (PDFs) for continuous, and cumulative distribution functions (CDFs) for both flavors.
Expected values of RVs and their distributions (a.k.a. expectations or just means), variances, and how to use PMFs, PDFs, and CDFs to compute probabilities that RVs will land in intervals or sets.
Independence (or lack thereof) between RVs.
If not, then you should first go back and review those topics before reading on.
In this chapter, and elsewhere in the book, we’ll often refer to specific probability distributions, like the exponential, uniform, triangular, etc. In days gone by books using probability notions contained lots of pages of distribution facts like definitions of PMFs, PDFs, and giving CDFs, expected values, variances, and so on, for many distributions. But this book does not have such a compendium since that material is readily available elsewhere, including the Simio documentation itself (described in Section 6.1.3), and on-line, such as https://en.wikipedia.org/wiki/List_of_probability_distributions, which in turn has links to web pages on well over 100 specific univariate distributions. Encyclopedic books, such as (Johnson, Kotz, and Balakrishnan 1994), (Johnson, Kotz, and Balakrishnan 1995), (Johnson, Kemp, and Kotz 2005), and (Evans, Hastings, and Peacock 2000), have been compiled. References to further material on distributions are in Section 6.1.3, along with some discussion of their properties, such as ranges.
In Section 2.1 we’ll describe the general structure, terminology, and notation for queueing systems. Section 2.2 states some important relationships among different output performance metrics of many queueing systems. We’ll quote a few specific queueing-system output results in Section 2.3, and briefly describe how to deal with networks of queues in Section 2.4. Finally, in Section 2.5 we’ll compare and contrast queueing theory vs. simulation as analysis tools, and show that each has pros and cons that dovetail nicely with each other (though on balance, we still like simulation better most of the time).
2.1 Queueing-System Structure and Terminology
A queueing system is one in which entities (like customers, patients, jobs, or messages) arrive, get served either at a single station or at several stations in turn, might have to wait in one or more queues for service, and then may leave (if they do leave the system is called open, but if they never leave and just keep circulating around within the system it’s called closed).
The urgent-care clinic described earlier, and in Figure 2.1, is modeled as an open queueing system. There are five separate service stations (Sign In, Registration, Trauma Rooms, Exam Rooms, and Treatment Rooms), each of which could be called a node in a network of multiserver queueing nodes (Registration has just a single server, but that’s a special case of multiserver). If there are multiple individual parallel servers at a queueing node (e.g., three for Exam Rooms), a single queue “feeds” them all, rather than having a separate queue for each single server, and we usually assume that the individual servers are identical in terms of their capabilities and service rates. The numbers by the arcs in Figure 2.1 give the probabilities that patients will follow those arcs. When coming out of a station where there’s a choice about where to go next (out of Sign In and Exam Rooms) we need to know these probabilities; when coming out of a station where all patients go to the same next station (out of Arrival, Registration, Trauma Rooms, Treatment Rooms) the 1.0 probabilities noted in the arcs are obvious, but we show them anyway for completeness. Though terminology varies, we’ll say that an entity is in queue if it’s waiting in the line but not in service, so right now at the Exam Rooms in Figure 2.1 there are four patients in queue and seven patients in the Exam-Room system; there are three patients in service at the Exam Rooms.
When a server finishes service on an entity and there are other entities in queue for that queueing node, we need to decide which specific entity in queue will be chosen to move into service next — this is called the queue discipline. You’re no doubt familiar with first-come, first-served (better known in queueing as first-in, first-out, or FIFO), which is common and might seem the “fairest.” Other queue disciplines are possible, though, like last-in, first-out (LIFO), which might represent the experience of chilled plates in a stack waiting to be used at a salad bar; clean plates are loaded onto the top, and taken from the top as well by customers. Some queue disciplines use priorities to pay attention to differences among entities in the queue, like shortest-job-first (SJF), also called shortest processing time (SPT). With an SJF queue discipline, the next entity chosen from the queue is one whose processing time will be lowest among all those then in queue (you’d have to know the processing times beforehand and assign them to individual entities), in an attempt to serve quickly those jobs needing only a little service, rather than making them wait behind jobs requiring long service, thereby hopefully improving (reducing) the average time in queue across all entities. Pity the poor big job, though, as it could be stuck near the back of the queue for a very long time, so whether SJF is “better” than FIFO might depend on whether you care more about average time in system or maximum (worst) time in system. A kind of opposite of SJF would be to have values assigned to each entity (maybe profit upon exiting service) and you’d like to choose the next job from the queue as the one with the highest value (time is money, you know). In a health-care system like that in Figure 2.1, patients might be initially triaged into several acuity levels, and the next patient taken from a queue would one in the most serious acuity-level queue that’s non-empty; within each acuity-level queue a tie-breaking rule, such as FIFO, would be needed to select among patients at the same acuity level.
Several performance measures (or output metrics) of queueing systems are often of interest:
The time in queue is, as you’d guess, the time that an entity spends waiting in line (excluding service time). In a queueing network like Figure 2.1, we could speak of the time in queue at each station separately, or added up for each patient over all the individual times in queue from arrival to the system on the upper left, to exit on the far right.
The time in system is the time in queue plus the time in service. Again, in a network, we could refer to time in system at each station separately, or overall from arrival to exit.
The number in queue (or queue length) is the number of entities in queue (again, not counting any entities who might be in service), either at each station separately or overall in the whole system. Right now in Figure 2.1 there are two patients in queue at Sign In, one at Registration, four at Exam Rooms, and none at both Trauma Rooms and Treatment Rooms; there are seven patients in queue in the whole system.
The number in system is the number of entities in queue plus in service, either at each station separately or overall in the whole system. Right now in Figure 2.1 there are four patients in system at Sign In, two at Registration, seven at Exam Rooms, one at Trauma Rooms, and two at Treatment Rooms; there are 16 patients in the whole system.
The utilization of a server (or group of parallel identical servers) is the time-average number of individual servers in the group who are busy, divided by the total number of servers in the group. For instance, at Exam Rooms there are three servers, and if we let \(B_E(t)\) be the number of the individual exam rooms that are busy (occupied) at any time \(t\), then the utilization is \[\begin{equation} \frac{\int_0^h B_E(t) dt} {3h}, \tag{2.1} \end{equation}\] where \(h\) is the length (or horizon) of time for which we observe the system in operation.
With but very few exceptions, the results available from queueing theory are for steady-state (or long-run, or infinite-horizon) conditions, as time (real or simulated) goes to infinity, and often just for steady-state averages (or means). Here’s common (though not universal) notation for such metrics, which we’ll use:
\(W_q=\) the steady-state average time in queue (excluding service times) of entities (at each station separately in a network, or overall across the whole network).
\(W=\) the steady-state average time in system (including service times) of entities (again, at each station separately or overall).
\(L_q=\) the steady-state average number of entities in queue (at each station separately or overall). Note that this is a time average, not the usual average of a discrete list of numbers, so might require a bit more explanation. Let \(L_q(t)\) be the number of entities in queue at time instant \(t\), so \(L_q(t) \in \{0, 1, 2, \ldots\}\) for all values of continuous time \(t\). Imagine a plot of \(L_q(t)\) vs. \(t\), which would be a piecewise-constant curve at levels 0, 1, 2, … , with jumps up and down at those time instants when entities enter and leave the queue(s). Over a finite time horizon \([0, h]\), the time-average number of entities in queue(s) (or the time-average queue length if we’re talking about just a single queue) will be \(\overline{L_q}(h) = \int_0^h L_q(t) dt/h\), which is a weighted average of the levels 0, 1, 2, … of \(L_q(t)\), with the weights being the proportion of time that \(L_q(t)\) spends at each level. Then \(L_q = \lim_{h \rightarrow \infty} \overline{L_q}(h)\).
\(L=\) the steady-state average number of entities in system (at each station separately or overall). As with \(L_q\), this is a time average, and is indeed defined similarly to \(L_q\), with \(L(t)\) defined as the number of entities in the system (in queue plus in service) at time \(t\), and then dropping the subscript \(q\) throughout the discussion.
\(\rho=\) the steady-state utilization of a server or group of parallel identical servers, typically for each station separately, as defined in equation (2.1) above for the Exam-Rooms example, but after letting \(h \rightarrow \infty\).
Much of queueing theory over the decades has been devoted to finding the values of these five steady-state average metrics, and is certainly far beyond our scope here. We will mention, though, that due to its very special property (the memoryless property), the exponential distribution is critical in many derivations and proofs. For instance, in the simplest queueing models, interarrival times (times between the arrivals of two successive entities to the system) are often assumed to have an exponential distribution, as are individual service times. In more advanced models, those distributions can be generalized to variations of the exponential (like Erlang, an RV that is the sum of independent and identically distributed (IID) exponential RVs), or even to general distributions; with each step in the generalization, though, the results become more complex both to derive and to apply.
Finally, there’s a standard notation to describe multiserver queueing stations, sometimes called Kendall’s notation, which is compact and convenient, and which we’ll use: \[A/B/c/k.\] An indication of the arrival process or interarrival-time distribution is given by \(A\). The service-time RVs are described by \(B\). The number of parallel identical servers is \(c\) (so \(c=3\) for the Exam Rooms in Figure 2.1, and \(c=1\) for Registration). The capacity (i.e., upper limit) on the system (including in queue plus in service) is denoted by \(k\); if there’s no capacity limit (i.e., \(k = \infty\)), then the \(/\infty\) is usually omitted from the end of the notation. Kendall’s notation is sometimes expanded to indicate the nature of the population of the input entities (the calling population), and the queue discipline, but we won’t need any of that. Some particular choices for \(A\) and \(B\) are of note. Always, \(M\) (for Markovian, or maybe memoryless) means an exponential distribution for either the interarrival times or the service times. Thus the \(M/M/1\) queue has exponential interarrival times, exponential service times (assumed independent of the interarrival times), and just a single server; \(M/M/3\) would describe the Exam Rooms component in Figure 2.1 if we knew that the interarrival times to it (coming out of Registration) and the Exam-Room service times were exponential. For an Erlang RV composed of the sum of \(m\) IID exponential RVs, \(E_m\) is common notation, so an \(M/E_3/2/10\) system would have exponential interarrival times, 3-Erlang service times, two parallel identical servers, and a limit of ten entities in the system at any one time (so a maximum of eight in the queue). The notation \(G\) is usually used for \(A\) or \(B\) when we want to allow a general interarrival-time or service-time distribution, respectively.
2.2 Little’s Law and Other Relations
There are several important relationships among the steady-state average metrics \(W_q\), \(W\), \(L_q\), and \(L\), defined in Section 2.1, which make computing (or estimating) the rest of them fairly simple if you know (or can estimate) any one of them. In this section we’re thinking primarily of just a single multiserver queueing station (like just the Exam Rooms in Figure 2.1 in isolation). Further notation we’ll need is \(\lambda\) = the arrival rate (which is the reciprocal of the expected value of the interarrival-time distribution), and \(\mu\) = the service rate of an individual server, not a group of multiple parallel identical servers (so \(\mu = 1/E(S)\), where \(S\) is an RV representing an entity’s service time in an individual server).
The most important of these relationships is Little’s law, the first version of which was derived in (Little 1961), but it’s been generalized repeatedly, e.g. (Stidham 1974); recently it celebrated its 50th anniversary ((Little 2011)). Stated simply, Little’s law is just \[L=\lambda W\] with our notation from above. In our application we’ll consider this just for a single multiserver queueing station, but be aware that it does apply more generally. The remarkable thing about Little’s law is that it relates a time average (\(L\) on the left-hand side) to an entity-based observational average (\(W\) on the right-hand side).
More physically intuitive than Little’s law is the relationship \[W = W_q + E(S),\] where we assume that we know at least the expected value \(E(S)\) of the service-time distribution, if not the whole distribution. This just says that your expected time in system is your expected time in queue plus your expected service time. This relationship, together with \(L=\lambda W\) and \(L_q=\lambda W_q\), allows you to get any of \(W_q\), \(W\), \(L_q\), and \(L\) if you know just one of them. For instance, if you know (or can estimate) \(W_q\), then just substituting yields \(L = \lambda (W_q + E(S))\); likewise, if you know \(L\), then after a little algebra you get \(W_q = L/\lambda - E(S)\).
2.3 Specific Results for Some Multiserver Queueing Stations
In this section we’ll just list formulas from the literature for a few multiserver queueing stations, i.e., something like the Exam Rooms in Figure 2.1, rather than an entire network of queues overall as shown across that entire figure. Remember, you can use Little’s law and other relations from Section 2.2 to get the other typical steady-state average metrics. Throughout, \(\rho = \lambda/(c \mu)\) is the utilization of the servers as a group (recall that \(c\) is the number of parallel identical servers at the queueing station); higher values of \(\rho\) generally portend more congestion. For all of these results (and throughout most of queueing theory), we need to assume that \(\rho < 1\) (\(\rho\le 1\) isn’t good enough) in order for any of these results to be valid, since they’re all for steady state, so we must know that the system will not “explode” over the long run with the number of entities present growing without bound — the servers, as a group, need to be able to serve entities at least as fast as they’re arriving.
In addition to just the four specific models considered here, there are certainly other such formulas and results for other queueing systems, available in the vast queueing-theory literature mentioned at the beginning of this chapter. However, they do tend to get quite complicated quite quickly, and in some cases are not really closed-form formulas, but rather equations involving the metrics you want, which you then need to “solve” using various numerical methods and approximations (as is actually the case with our fourth example below).
2.3.1 M/M/1
Perhaps the simplest of all queueing systems, we have exponential interarrival times, exponential service times, and just a single server.
The steady-state average number in system is \(L = \rho/(1-\rho)\). Remember that \(\rho\) is the mean arrival rate \(\lambda\) divided by the mean service rate \(\mu\) if there’s just a single server. Certainly, \(L\) can be expressed in different ways, like \[L = \frac{\lambda}{1/E(S) - \lambda}.\] If we know \(L\), we can then use the relations in Section 2.2 to compute the other metrics \(W_q\), \(W\), and \(L_q\).
2.3.2 M/M/c
Again, both interarrival times and services times follow exponential distributions, but now we have \(c\) parallel identical servers being fed by a single queue.
First, let \(p(n)\) be the probability of having \(n\) entities in the system in steady state. The only one of these we really need is the steady-state probability that the system is empty, which turns out to be \[ p(0) = \frac{1} {\frac{(c \rho)^c}{c! (1-\rho)} + \sum_{n=0}^{c-1}\frac{(c \rho)^n}{n!}}, \] a little complicated but is just a formula that can be computed, maybe even in a spreadsheet, since \(c\) is finite, and often fairly small. (For any positive integer \(j\), \(j! = j \times (j-1) \times (j-2) \times \cdots \times 2 \times 1\), and is pronounced “\(j\) factorial” — not by shouting “\(j\).” Mostly for convenience, \(0!\) is just defined to be 1.) Then, \[ L_q = \frac{\rho(c \rho)^c p(0)} {c! (1-\rho)^2}, \] from which you could get, for example, \(L = L_q + \lambda/\mu\) along with the other metrics via the relationships in Section 2.2.
Though the formulas above for the \(M/M/c\) are all closed-form (i.e., you can in principle plug numbers into them), they’re a little complicated, especially the summation in the denominator in the expression for \(p(0)\) unless \(c\) is very small. So we provide a small command-line program mmc.exe (see Appendix Section C.4.2 for the download URL), to do this for values that you specify for the arrival rate \(\lambda\), the service rate \(\mu\), and the number of servers \(c\). To invoke mmc.exe you need to run the Microsoft Windows Command Prompt window (usually via the Windows Start button, then Programs or All Programs, then in the Accessories folder). It’s probably simplest to move the mmc.exe file to the “root” drive (usually C:) on your system, and then in the Command Prompt window, type cd .. repeatedly until the prompt reads just C:\(\backslash >\). If you then type just mmc at the prompt you’ll get a response telling you what the syntax is, as shown at the top of Figure 2.2. Then, type mmc followed by the values you want for \(\lambda\), \(\mu\), and \(c\), separated by any number of blank spaces. The program responds with the steady-state queueing metrics for this system, assuming that the values you specified result in a stable queue, i.e., values for which \(\rho < 1\). The resulting metrics are all for steady-state, using whatever time units you used for your input parameters (of course, \(\lambda\) and \(\mu\) must use the same time units, but that time unit could be anything and is not needed by mmc.exe).
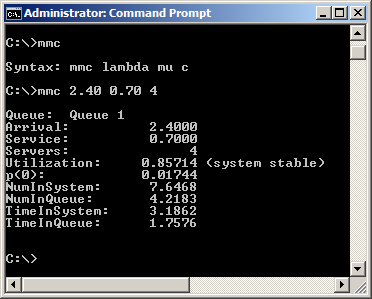
Figure 2.2: Example of using the mmc.cmd command-line program.
If you are a Python user, you can find a Python mmc module and examples at https://github.com/auie86/mmc. In addition to solving single-server systems, this module can be used to solve Jackson Network models discussed in Section 2.4.
2.3.3 M/G/1
This model once again has exponential interarrival times, but now the service-time distribution can be anything; however, we’re back to just a single server. This might be more realistic than the \(M/M/1\) since exponential service times, with a mode (most likely value) of zero, are usually far-fetched in reality.
Let \(\sigma\) be the standard deviation of the service-time RV \(S\), so \(\sigma^2\) is its variance; recall that \(E(S) = 1/\mu\). Then \[ W_q = \frac{\lambda(\sigma^2 + 1/\mu^2)}{2(1 - \lambda/\mu)}. \] From this (known as the Pollaczek-Khinchine formula), you can use Little’s law and the other relations in Section 2.2 to get additional output metrics, like \(L\) = the steady-state average number in system.
Note that \(W_q\) here depends on the variance \(\sigma^2\) of the service-time distribution, and not just on its mean \(1/\mu\); larger \(\sigma^2\) implies larger \(W_q\). Even the occasional extremely long service time can tie up the single server, and thus the system, for a long time, with new entities arriving all the while, thus causing congestion to build up (as measured by \(W_q\) and the other metrics). And the higher the variance of the service time, the longer the right tail of the service-time distribution, and thus the better the chance of encountering some of those extremely long service times.
2.3.4 G/M/1
This final example is a kind of reverse of the preceding one, in that now interarrival times can follow any distribution (of course, they have to be positive to make sense), but service times are exponential. We just argued that exponential service times are far-fetched, but this assumption, especially its memoryless property, is needed to derive the results below. And, there’s just a single server. This model is more complex to analyze since, unlike the prior three models, knowing the number of entities present in the system is not enough to predict the future probabilistically, because the non-exponential (and thus non-memoryless) interarrival times imply that we also need to know how long it’s been since the most recent arrival. As a result, the “formula” isn’t really a formula at all, in the sense of being a closed-form plug-and-chug situation. For more on the derivations, see, for example, (Gross et al. 2008) or (Ross 2010).
Let \(g(t)\) be the density function of the interarrival-time distribution; we’ll assume a continuous distribution, which is reasonable, and again, taking on only positive values. Recall that \(\mu\) is the service rate (exponential here), so the mean service time is \(1/\mu\). Let \(z\) be a number between 0 and 1 that satisfies the integral equation
\[\begin{equation} z = \int_0^{\infty} e^{-\mu t (1 - z)} g(t) dt. \tag{2.2} \end{equation}\]
Then \[ W = \frac{1}{\mu (1 - z)}, \] and from that, as usual, we can get the other metrics via the relations in Section 2.2.
So the question is: What’s the value of \(z\) that satisfies equation (2.2)? Unfortunately, (2.2) generally needs to be solved for \(z\) by some sort of numerical method, such as Newton-Raphson iterations or another root-finding algorithm. And the task is complicated by the fact that the right-hand side of (2.2) involves an integral, which itself has under it the variable \(z\) we’re seeking!
So in general, this is not exactly a “formula” for \(W\), but in some particular cases of the interarrival-time distribution, we might be able to manage something. For instance, if interarrivals have a continuous uniform distribution on \([a,b]\) (with \(0 \le a < b\)), then their PDF is \[ g(t) = \left\{ \begin{array}{l l} 1/(b-a) & \quad \mbox{if $a \le t \le b$}\\ 0 & \quad \mbox{otherwise}\\ \end{array} \right.. \] Substituting this into (2.2) results in \[ z = \int_a^b e^{-\mu t (1 - z)} \frac{1}{b-a} dt, \] which, after a little calculus and algebra, turns out to amount to \[\begin{equation} z = -\frac{1}{\mu (b-a)(1-z)}\left[ e^{-\mu(1-z)b} - e^{-\mu(1-z)a}\right], \tag{2.3} \end{equation}\] and this can be solved for \(z\) by a numerical method.
Microsoft Excel’s built-in Goal Seek capability, basically a numerical root-finder, might work. In Excel 2007/2010 Goal Seek is on the Data ribbon/tab, under the What-If Analysis button; in other versions of Excel it may be located elsewhere. In the file Uniform_M_1_queue_numerical_solution.xls, which you can download as specified in Appendix C, we’ve set this up for this Uniform/\(M/1\) queue; see Figure 2.3.
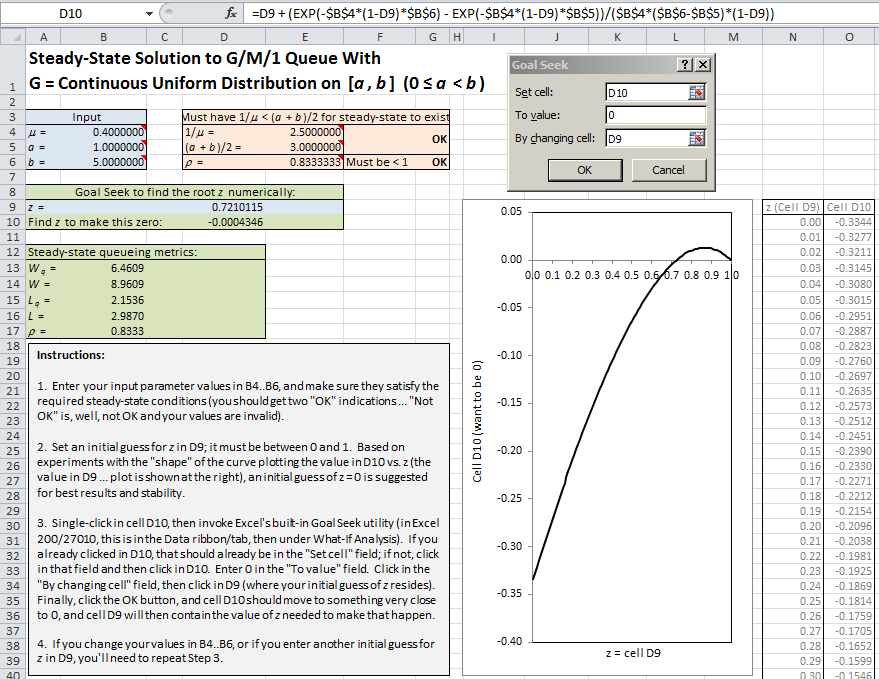
Figure 2.3: Excel spreadsheet using Goal Seek to solve for stead-state queueing metrics.
The formula in cell D10 (showing at the top of the figure) contains equation (2.3), except written as its left-hand side minus its right-hand side, so we use Goal Seek to find the value of \(z\) (in cell D9) that makes this difference in cell D10 (approximately) 0. You need to supply an initial “guess” at the root-finding value of \(z\) (which must be between 0 and 1) and enter your guess in cell D9; based on experimentation with the shape of the curve in cell D10 as a function of \(z\) in cell D9, it appears that initializing with \(z = 0\) in cell D9 provides the most robust and stable results. The completed Goal Seek dialog is shown, and the results on the left are after it has run to completion. After approximating the required solution for \(z\) and confirming that cell D10 is (close to) 0, the spreadsheet also computes the standard steady-state queueing metrics. The text box at the bottom contains more detailed instructions for use of this spreadsheet model.
2.4 Queueing Networks
Queueing networks are composed of nodes, each being a multiserver queueing station (like Registration and Treatment Rooms in the urgent-care clinic of Figure 2.1), and connected by arcs representing possible paths of entity travel from one node to another (or from outside the system to a node, or from a node to exit the system). Entities can enter from outside the system into any node, though in our clinic they enter only to the Sign In node. Entities can also exit the system from any node, as they do from the Exam Rooms and Treatment Rooms nodes in our clinic. Internally, when an entity leaves a node it can go to any other node, with branching probabilities as in Figure 2.1; from Sign In they go to Registration with probability 0.9, and to Trauma Rooms with probability 0.1, etc. It’s possible that all entities exiting a node go to the same place; such is the case out of the Registration and Trauma Rooms nodes.
We’ll assume that all arrival processes from outside are independent of each other with exponential interarrival times (called a Poisson process since the number of entities arriving in a fixed time period follows the discrete Poisson distribution); in our clinic we have only one arrival source from outside, and all entities from it go to the Sign In node. We’ll further assume that the service times everywhere are exponentially distributed, and independent of each other, and of the input arrival processes. And, we assume that all queue capacities are infinite. Finally, we’ll assume that the utilization (a.k.a. traffic intensity) \(\rho\) at each node is strictly less than 1, so that the system does not explode anywhere in the long run. With all these assumptions, this is called a Jackson network (first developed in (Jackson 1957)), and a lot is known about it.
In our clinic, looking at just the Sign In node, this is an \(M/M/2\) with arrival rate that we’ll denote \(\lambda_{\textrm{SignIn}}\), which would need to be given (so the interarrival times are IID exponential with mean \(1/\lambda_{\textrm{SignIn}}\)). Remarkably, in stable \(M/M/c\) queueing stations, the output is also a Poisson process with the same rate as the input rate, \(\lambda_{\textrm{SignIn}}\) in this case. In other words, if you stand at the exit from the Sign-In station, you’ll see the same probabilistic behavior that you see at the entrance to it. Now in this case that output stream is split by an independent toss of a (biased) coin, with each patient’s going to Registration with probability 0.9, and to Trauma Rooms with probability 0.1. So we have two streams going out, and it turns out that each is also an independent Poisson process (this is called decomposition of a Poisson process), and at rate \(0.9\lambda_{\textrm{SignIn}}\) into Registration and \(0.1\lambda_{\textrm{SignIn}}\) into Trauma Rooms. Thus Registration can be analyzed as an \(M/M/1\) queue with arrival rate \(0.9\lambda_{\textrm{SignIn}}\), and Trauma Rooms can be analyzed as an \(M/M/2\) queue with arrival rate \(0.1\lambda_{\textrm{SignIn}}\). Furthermore, all three of the nodes we’ve discussed so far (Sign In, Registration, and Trauma Rooms) are probabilistically independent of each other.
Proceeding in this way through the network, we can analyze all the nodes as follows:
Sign In: \(M/M/2\) with arrival rate \(\lambda_{\textrm{SignIn}}\).
Registration: \(M/M/1\) with arrival rate \(0.9\lambda_{\textrm{SignIn}}\).
Trauma Rooms: \(M/M/2\) with arrival rate \(0.1\lambda_{\textrm{SignIn}}\).
Exam Rooms: \(M/M/3\) with arrival rate \(0.9\lambda_{\textrm{SignIn}}\).
Treatment Rooms: \(M/M/2\) with arrival rate \[(0.9)(0.6)\lambda_{\textrm{SignIn}} + 0.1\lambda_{\textrm{SignIn}} = 0.64\lambda_{\textrm{SignIn}}.\] The incoming process to Treatment Rooms is called the superposition of two independent Poisson processes, in which case we simply add their rates together to get the effective total incoming rate (and the superposed process is again a Poisson process).
So for each node separately, we could use the formulas for the \(M/M/c\) case (or the command-line program mmc.exe) in Section 2.3 to find the steady-state average number and times in queue and system at each node separately.
You can do the same sort of thing to get the utilizations (traffic intensities) at each node separately. We know from the above list what the incoming rate is to each node, and if we know the service rate of each individual server at each node, we can compute the utilization there. For instance, let \(\mu_{\textrm{Exam}}\) be the service rate at each of the three parallel independent servers at Exam Rooms. Then the “local” traffic intensity at Exam Rooms is \(\rho_{\textrm{Exam}} = 0.9\lambda_{\textrm{SignIn}}/(3\mu_{\textrm{Exam}})\). Actually, these utilization calculations remain valid for any distribution of interarrival and service-times (not just exponential), in which case the arrival and service rates are defined as simply the reciprocals of the expected value of an interarrival and service-time RV, respectively.
As mentioned above, though our urgent-care-clinic example doesn’t have it, there could be more Poisson input streams from outside the system arriving directly into any of the nodes; the overall effective input rate to a node is just the sum of the individual input rates coming into it. There could also be self-loops; for example out of Treatment Rooms, it could be that only 80% of patients exit the system, and the other 20% loop directly back to the input for Treatment Rooms (presumably for further treatment); in such a case, it may be necessary to solve a linear equation for, say, \(\lambda_{\textrm{TreatmentRooms}}\). For the analysis of this section to remain valid, though, we do need to ensure that the “local” traffic intensity at each of the nodes stays strictly below 1. An example of a a generic network with these characteristics is given next.
Consider the queueing network shown in Figure 2.4.
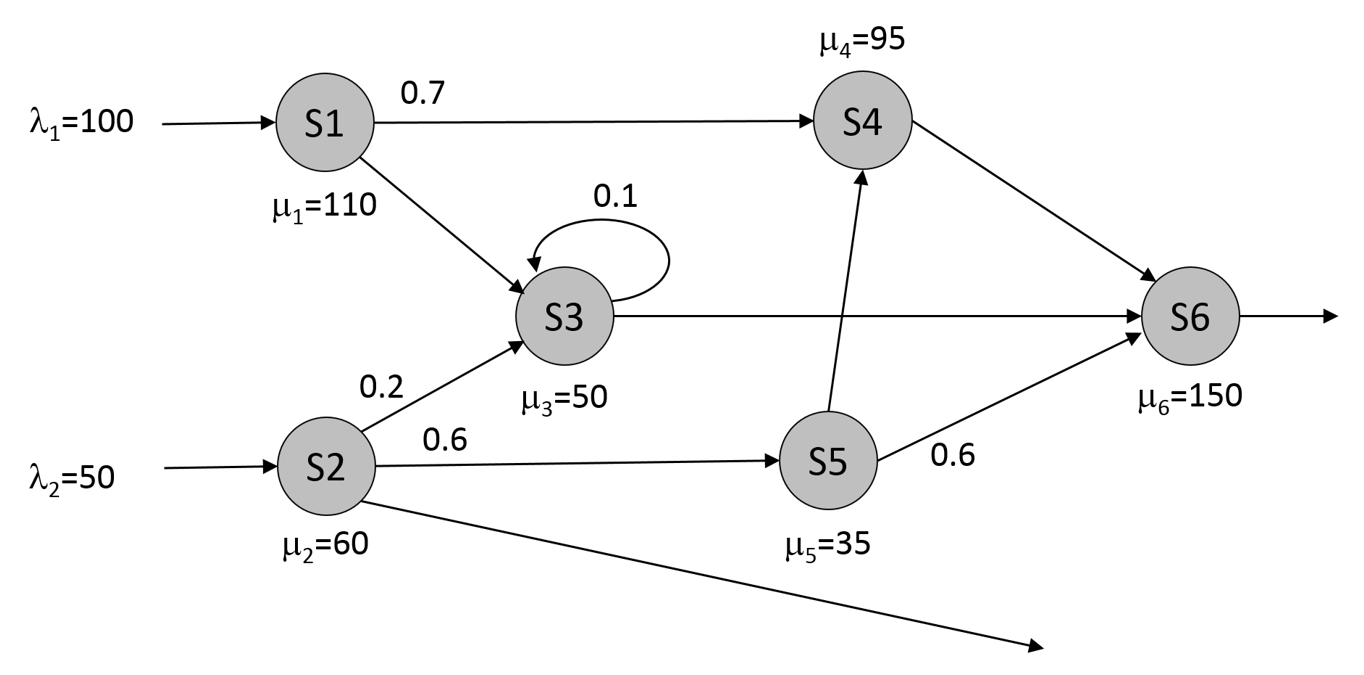
Figure 2.4: Queueing network example. Assume that \(c=1\) for all stations.
Our interest is in determining the steady-state values for the average number of entities in the system (\(L\)), the average time that an entity spends in the system (\(W\)) and the server traffic intensities (\(\rho_i\)). The first step is to determine the arrival rates for each server. If a server’s traffic intensity is strictly less than 1, the departure rate is exactly the arrival rate – we’ll assume that this is true for all servers now and will verify this as we go. The arrival rates can be computed as: \[\begin{align*} \lambda_1 &= 100 \\ \lambda_2 &= 50 \\ \lambda_3 &= \left(\frac{1}{0.9}\right)(0.3\lambda_1+0.2\lambda_2) \\ \lambda_4 &= 0.7\lambda_1+0.4\lambda_5 \\ \lambda_5 &= 0.6\lambda_2 \\ \lambda_6 &= \lambda_4+0.9\lambda_3+0.6\lambda_5 \end{align*}\] Given the arrival rates, the service rates shown in Figure 2.4, and the assumption that \(c=1\) for all servers, we can apply the formulae from Section 2.3 to find \(L_j\), \(W_j\), and \(\rho_j\) for each server, \(j\) (see Table 2.1).
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| \(\lambda_j\) | 100.00 | 50.00 | 44.44 | 82.00 | 30.00 | 140.00 |
| \(\mu_j\) | 110.00 | 60.00 | 50.00 | 95.00 | 35.00 | 150.00 |
| \(\rho_j\) | 0.91 | 0.83 | 0.89 | 0.86 | 0.86 | 0.93 |
| \(L_j\) | 10.00 | 5.00 | 8.00 | 6.31 | 6.00 | 14.00 |
| \(W_j\) | 0.10 | 0.10 | 0.18 | 0.08 | 0.20 | 0.10 |
Since all of the local traffic intensities are strictly less that 1 (the assumption that we made earlier in order to find the arrival rates), we can find the overall average number in system, \(L\) and overall average time in system \(W\) for the network as:
\[\begin{align*} L &= \sum_{j=1}^6 L_i \\ W &= \frac{L}{\lambda_1 + \lambda_2} \end{align*}\]
As we will see later in the book, this type of analysis can be very useful for model verification even if the standard queueing assumptions aren’t met for a given system that we wish to simulate.
2.5 Queueing Theory vs. Simulation
The nice thing about queueing-theoretic results is that they’re exact, i.e., not subject to statistical variation (though in some cases where numerical analysis might be involved to find the solution, as in Section 2.3.4 for the \(G/M/1\) queue, there could be roundoff error). As you’ll soon see, simulation results are not exact, and do have statistical uncertainty associated with them, which we do need to acknowledge, measure, and address properly.
But queueing theory has other shortcomings of its own, mostly centered around the assumptions we need to make in order to derive formulas such as those in Section 2.3. In many real-world situations those assumptions will likely be simply incorrect, and it’s hard to say what impact that might have on correctness of the results, and thus model validity. Assuming exponential service times seems particularly unrealistic in most situations, since the mode of the exponential distribution is zero — when you go to, say, airport security, do you think that it’s most likely that your service time will be very close to zero, as opposed to having a most likely value of some number that’s strictly greater than zero? And as we mentioned, such results are nearly always only for steady-state performance metrics, so don’t tell you much if you’re interested in short-term (or finite-horizon or transient) performance. And, queueing-theoretic results are not universally available for all interarrival-time and service-time distributions (recall the mathematical convenience of the memoryless exponential distribution), though approximation methods can be quite accurate.
Simulation, on the other hand, can most easily deal with short-term (or finite-horizon) time frames. In fact, steady-state is harder for simulation since we have to run for very long times, and also worry about biasing effects of initial conditions that are uncharacteristic of steady state. And when simulating, we can use whatever interarrival- and service-time distributions seem appropriate to fit the real system we’re studying (see Sections 6.1 and 6.2), and in particular we have no need to assume that anything has an exponential distribution unless it happens to appear that way from the real-world data. Thus, we feel that simulation models stand a better chance of being more realistic, and thus more valid, models of reality, not to mention that their structure can go far beyond standard queueing models into great levels of complexity that render completely hopeless any kind of exact mathematical analysis. The only real downside to simulation is that you must remember that simulation results are statistical estimates, so must be analyzed with proper statistical techniques in order to be able to draw justified and precise conclusions, a point to which we’ll return often in the rest of this book. In fact, the urgent-care clinic shown in Figure 2.1 and discussed throughout this chapter will be simulated (and properly statistically analyzed, of course), all in Simio, in a much more realistic framework in Chapter 9.
2.6 Problems
For an \(M/M/1\) queue with mean interarrival time 1.25 minutes and mean service time 1 minute, find all five of \(W_q\), \(W\), \(L_q\), \(L\), and \(\rho\). For each, interpret in words. Be sure to state all your units (always!), and the relevant time frame of operation.
Repeat Problem 1, except assume that the service times are not exponentially distributed, but rather (continuously) uniformly distributed between \(a=0.1\) and \(b=1.9\). Note that the expected value of this uniform distribution is \((a+b)/2 = 1\), the same as the expected service time in Problem 1. Compare all five of your numerical results to those from Problem 1 and explain intuitively with respect to this change in the service-time distribution (but with its expected value remaining at 1). Hint: In case you’ve forgotten, or your calculus has rusted completely shut, or you haven’t already found it with a web search, the standard deviation of the continuous uniform distribution between \(a\) and \(b\) is \(\sqrt{(b-a)^2/12}\) (that’s right, you always divide by 12 regardless of what \(a\) and \(b\) are … the calculus just works out that way).
Repeat Problem 1, except assume that the service times are triangularly distributed between \(a = 0.1\) and \(b = 1.9\), and with the mode at \(m=1.0\). Compare all five of your results to those from Problems 1 and 2. Hint: The expected value of a triangular distribution between \(a\) and \(b\), and with mode \(m\) (\(a < m < b\)), is \((a + m + b)/3\), and the standard deviation is \(\sqrt{(a^2 + m^2 + b^2 -am - ab - bm)/18}\) … do you think maybe it’s time to dust off that calculus book (or, at least hone your web-search skills)?
In each of Problems 1, 2, and 3, suppose that we’d like to see what would happen if the arrival rate were to increase in small steps; maybe a single-server barbershop would like to increase business by some advertising or coupons. Create a spreadsheet or a computer program (if you haven’t already done so to solve those problems), and re-evaluate all five of \(W_q\), \(W\), \(L_q\), \(L\), and \(\rho\), except increasing the arrival rate by 1% over its original value, then by 2% over its original value, then by 3% over its original value, and so on until the system becomes unstable (\(\rho \ge 1\)). Make plots of each of the five metrics as functions of the percent increase in the arrival rate. Discuss your findings.
Repeat Problem 1, except for an \(M/M/3\) queue with mean interarrival time 1.25 minutes and mean service time 3 minutes at each of the three servers. Hint: You might want to consider creating a computer program or spreadsheet, or use
mmc.exe.In Problem 5, increase the arrival rate in the same steps as in Problem 4, and again evaluate all of \(W_q\), \(W\), \(L_q\), \(L\), and \(\rho\) at each step. Continue incrementing the arrival rate in 1% steps until you reach 100% over the original rate (i.e., doubling the rate) and adding servers as necessary (but keeping the minimum number of servers to achieve stability).
Show that the formula for \(L_q\) for the \(M/M/c\) queue in Section 2.3 includes the \(M/M/1\) as a special case.
In the urgent-care clinic of Figure 2.1, suppose that the patients arrive from outside into the clinic (coming from the upper right corner of the figure and always into the Sign In station) with interarrival times that are exponentially distributed with mean 6 minutes. The number of individual servers at each station and the branching probabilities are all as shown in Figure 2.1. The service times at each node are exponentially distributed with means (all in minutes) of 3 for Sign In, 5 for Registration, 90 for Trauma Rooms, 16 for Exam Rooms, and 15 for Treatment Rooms. For each of the five stations, compute the “local” traffic intensity \(\rho_{Station}\) there. Will this clinic “work,” i.e., be able to handle the external patient load? Why or why not? If you could add a single server to the system, and add it to any of the five stations, where would you add it? Why? Hint: Unless you like using your calculator, a spreadsheet or computer program might be good, or perhaps use
mmc.exe.In Problem 8, for each of the five stations, compute each of \(W_q\), \(W\), \(L_q\), \(L\), and \(\rho\), and interpret in words. Would you still make the same decision about where to add that extra single resource unit that you did in Problem 8? Why or why not? (Remember these are sick people, some of them seriously ill, not widgets being pushed through a factory.) Hint: Unless you really, really, really like using your calculator, a spreadsheet or computer program might be very good, or maybe you could use
mmc.exe.In Problems 8 and 9 (and without the extra resource unit), the inflow rate was ten per hour, the same as saying that the interarrival times have a mean of 6 minutes. How much higher could this inflow rate go and have the whole clinic still “work” (i.e., be able to handle the external patient load), even if only barely? Don’t do any more calculations than necessary to answer this problem. If you’d like to get this really exact, you might consider looking up a root-finding method and program it into your computer program (if you wrote one), or use the Goal Seek capability in Excel (if you created an Excel spreadsheet).
In Problems 8 and 9 (and without the extra resource unit), the budget’s been cut and we need to eliminate one of the ten individual servers across the clinic; however, we have to keep at least one at each station. Where would this cut be least damaging to the system’s operation? Could we cut two servers and expect the system still to “work?” More than two?